The Unit 2 Equations and Inequalities Answer Key is an indispensable resource for students seeking to master the intricacies of algebraic equations and inequalities. This guide provides a comprehensive overview of the concepts, methods, and applications of equations and inequalities, empowering learners to tackle complex mathematical challenges with confidence and accuracy.

Delving into the realm of equations and inequalities, this answer key unravels the mysteries of solving equations, graphing inequalities, and applying these mathematical tools to real-world scenarios. By exploring various equation and inequality types, students gain a deep understanding of their properties and solution techniques.

Introduction

In unit 2 of mathematics, students delve into the fascinating world of equations and inequalities. Understanding these concepts is crucial for developing problem-solving skills, analytical thinking, and mathematical literacy.

An answer key is an indispensable tool that helps students check their solutions, identify errors, and reinforce their understanding. By utilizing the answer key effectively, students can improve their accuracy and gain confidence in solving equations and inequalities.

Types of Equations and Inequalities

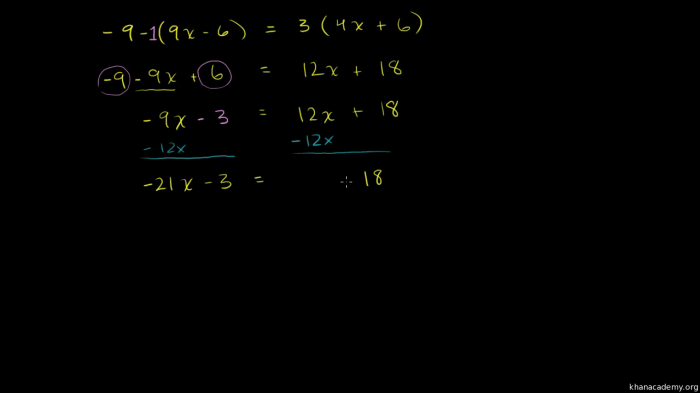
Equations

• Linear equations: Equations that can be written in the form Ax + B = C, where A, B, and C are constants.
• Quadratic equations: Equations that can be written in the form ax ²+ bx + c = 0, where a, b, and c are constants and a ≠ 0.

Inequalities

• Linear inequalities: Inequalities that can be written in the form Ax + B < C, Ax + B > C, Ax + B ≤ C, or Ax + B ≥ C, where A, B, and C are constants.
• Quadratic inequalities: Inequalities that can be written in the form ax²+ bx + c < 0, ax²+ bx + c > 0, ax ²+ bx + c ≤ 0, or ax ²+ bx + c ≥ 0, where a, b, and c are constants and a ≠ 0.

Solving Equations

Steps for Solving Equations

1. Isolate the variable on one side of the equation.
2. Simplify both sides of the equation.
3. Check the solution by substituting it back into the original equation.

Methods for Solving Equations

• Using inverse operations: Adding or subtracting the same value from both sides, multiplying or dividing both sides by the same nonzero value.
• Factoring: Breaking down an expression into smaller factors.
• Substitution: Substituting a known value for a variable in an equation.

Equations with Variables on Both Sides

To solve equations with variables on both sides, first combine like terms on each side. Then, isolate the variable on one side using inverse operations or factoring.

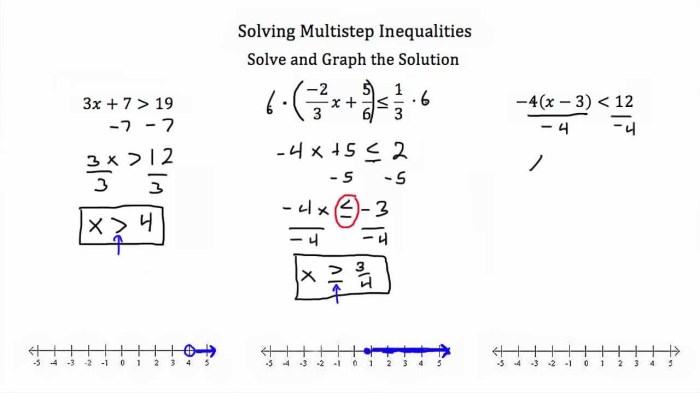
Solving Inequalities

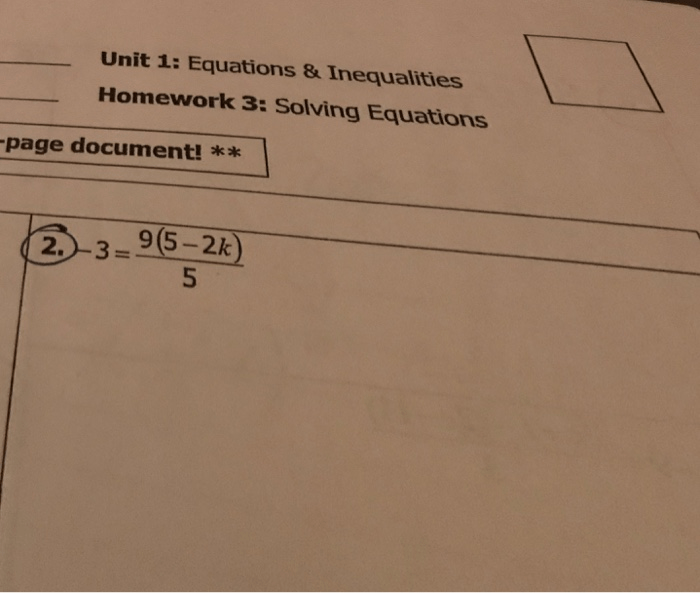
Concept of Inequalities

Inequalities are mathematical statements that compare two expressions using symbols such as <, >, ≤, and ≥. Unlike equations, inequalities do not have a single solution but rather a range of solutions.

Steps for Solving Inequalities, Unit 2 equations and inequalities answer key

1. Solve the inequality as if it were an equation.
2. Identify the critical points where the inequality changes direction.
3. Test points in each interval to determine the sign of the expression.
4. Write the solution as an interval or union of intervals.

Solving Compound Inequalities and Inequalities Involving Absolute Value

• Compound inequalities: Inequalities that combine two or more inequalities using the words “and” or “or.”
• Inequalities involving absolute value: Inequalities that contain an absolute value expression.

Applications of Equations and Inequalities: Unit 2 Equations And Inequalities Answer Key

Real-World Applications

Equations and inequalities have numerous applications in various fields, including:

• Physics: Modeling motion, forces, and energy.
• Economics: Analyzing supply and demand, calculating profit, and forecasting economic trends.
• Engineering: Designing structures, solving circuits, and optimizing systems.

Modeling and Solving Problems

Solving equations and inequalities helps us model real-world situations and solve problems by:

• Representing relationships between variables.
• Predicting outcomes based on given conditions.
• Determining optimal solutions.

Using the Answer Key

Importance of Checking Solutions

Using the answer key is crucial for students to check their solutions and identify errors. By comparing their answers to the provided solutions, students can:

• Verify their understanding of the concepts.
• Identify areas where they need further practice.
• Build confidence in their problem-solving abilities.

Tips for Effective Utilization

• Check solutions as soon as possible after completing a problem.
• Compare the solution to the answer key step by step.
• Analyze any errors to understand why they occurred.
• Use the answer key as a learning tool to reinforce concepts.

Additional Resources

For additional practice and support, students can access the following resources:

• Online platforms: Khan Academy, Mathway, Wolfram Alpha
• Worksheets: Available from textbooks, teachers, or online repositories
• Tutors or teachers: Seek help if needed to clarify concepts or resolve difficulties

Detailed FAQs

What is the significance of using an answer key for equations and inequalities?

An answer key provides instant feedback, allowing students to check the accuracy of their solutions and identify areas for improvement.

How can I effectively utilize the answer key to enhance my understanding?

Review the solutions provided in the answer key, paying attention to the steps involved and the underlying concepts. Use the key to identify common errors and reinforce your knowledge.

What types of equations and inequalities are covered in Unit 2?

Unit 2 typically covers linear equations, quadratic equations, systems of equations, and linear inequalities.